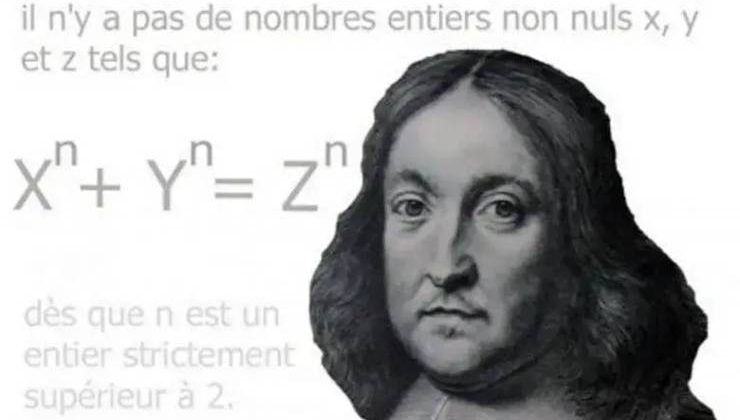
Fermat’ın Son Teoremi Hakkında

0

BEĞENDİM

ABONE OL

News

0

Fermat’ın Son Teoremi Hakkında​

Kurduğu pek çok teorem olmasına rağmen, bu kadar tanınmasındaki en önemli sebep, belki de bu son teoremi olmuştur. Fermat, Diophantus’un ‘Arithmetica’ kitabında, Pisagor üçgenlerinin anlatıldığı bir sayfayı okurken, sayfanın yanına, an + bn = cn eşitliğinin 2’den büyük ‘n’ değerleri için geçersiz olduğunu not düşer ve altına bir de not iliştirir:

“… Cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet!”

Fransız matematikçi Pierre de Fermat (piyer dö ferma)’nın 17. yüzyılda (1637) öne sürdüğü, fakat kanıtı ancak 1994 yılında İngiliz matematikçi Andrew Wiles tarafından verilen teoremdir. Fermat, hayatı boyunca kitap yazmaz. Matematikçilerle fazla görüşmez. Kurduğu teoremlerin hiçbirinin ispatını yapmaz, başkalarının bulması için bıraktığını söyler. Gerçekten de teoremleri, sonradan farklı bilim adamları tarafından ispatlanır. Ölümünden sonra, bulduğu teoremlerin unutulmasına sevdiklerinin gönlü razı gelmez. Fermat’ın vasiyeti var mıdır, bilinmez; ama geride bıraktığı oğlu tarafından derlenir toplanır ve kitap haline getirilir.

Kurduğu pek çok teorem olmasına rağmen, bu kadar tanınmasındaki en önemli sebep, belki de bu son teoremi olmuştur. Fermat, Diophantus’un ‘Arithmetica’ kitabında, Pisagor üçgenlerinin anlatıldığı bir sayfayı okurken, sayfanın yanına, an + bn = cn eşitliğinin 2’den büyük ‘n’ değerleri için geçersiz olduğunu not düşer ve altına bir de not iliştirir:

“… Cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet!”

Yani: “Bu teoremin müthiş bir ispatını buldum ama burada yazacak kadar yer yok!”

Teorem, ortaokul matematik bilgileriyle anlaşılacak kadar yalın olmasına karşılık öne sürülmesiyle kanıtlanması arasında geçen çok uzun sürede, pek çok ünlü matematikçi tarafından üzerinde uğraşılıp da kanıtlanamamış olmasıyla matematik tarihinde öne çıkmıştır.

Teoremısaca, eğer ‘n’ ikiden büyük bir tam sayıysa ve x, y, z sayıları pozitif tam sayılar ise; Fermat’ın ‘Son Teoremi’ ifadesinin sağlanamayacağını ifade eder. İfadenin n=1 ve n=2 durumlarında kolayca sağlanabileceğini görmek zor değildir. Biraz açmak gerekirse, n=2 durumu, ünlü Pisagor Teoremi ile yakından ilişkili olup x=3, y=4, z=5 veya x=5, y=12, z=13 tam sayı üçlüleriyle kolayca sağlanır. Bu sanının (artık teorem demek gerekiyor elbette) kanıtı için pek çok matematikçi uğraşmış, ancak başarısız olmuşlardır.

Ancak yakın tarihlere kadar çok büyük ‘n’ değerleri için bu sanının doğrulanmasına devam edilmiştir. Bu tür kısmi ilerlemelere yönelik çabalar, hiç beklenmedik bir zamanda İngiliz matematikçi Andrew Wiles’ın bir kanıt bulduğunu duyurmasıyla son bulmuştur. Ne var ki kısa sürede Andrew Wiles’ın kanıtında bir hata bulunmuş ve Andrew Wiles, uzun ve yorucu bir çabanın sonunda 1994 yılında uzmanlarca doğruluğu kabul gören bir kanıt vermeyi başarmıştır. Aslında Wiles’ın kanıtı, Fermat’ın son teoreminden daha güçlü bir ifadenin, Şimura-Taniyama Konjektürü’nün de doğruluğunu göstermiştir.

Söz konusu kanıt, Sayılar Teorisi’nin çok gelişkin tekniklerini kullanır.

Fermat, ispatı biliyor muydu?

Bundan emin değiliz. Arithmetica‘ya düştüğü not, bütün diğer çalışmaları gibi, matematikçilerin aklına bir çengel takar. Fakat ispatlanmasına rağmen, bu teoremi Fermat’ın da ispatlayabildiğinden matematikçiler de emin değil. Bu şüphenin sebebi, Fermat’ın yaşadığı yıllarda, Wiles’ın ispatında kullandığı yöntemlerin bilinmiyor olması. Fakat yine de matematikçiler emin değiller hocam…